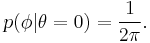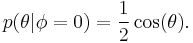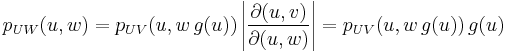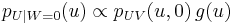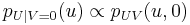Borel–Kolmogorov paradox

In probability theory, the Borel–Kolmogorov paradox (sometimes known as Borel's paradox) is a paradox relating to conditional probability with respect to an event of probability zero (also known as a null set). It is named after Émile Borel and Andrey Kolmogorov.

The paradox lies in the fact that a conditional distribution with respect to such an event is ambiguous unless it is viewed as an observation from a continuous random variable. Furthermore, it is dependent on how this random variable is defined.

Contents 1 A great circle puzzle 2 Explanation and implications 3 Further example 4 Notes 5 References and further reading

A great circle puzzle

Suppose that a random variable has a uniform distribution on a sphere. What is its conditional distribution on a great circle? Because of the symmetry of the sphere, one might expect that the distribution is uniform and independent of the choice of coordinates. However, two analyses give contradictory results:

1. If the coordinates are chosen so that the great circle is an equator (latitude θ = 0), the conditional distribution for a longitude Φ defined on the interval (–π,π) is ^[1]

2. If the great circle is a line of longitude with Φ = 0, the conditional distribution for θ on the interval (–π/2,π/2) is ^[1]

One distribution is uniform, the other is not. Yet both seem to be referring to the same great circle in different coordinate systems.

Many quite futile arguments have raged - between otherwise competent probabilists - over which of these results is 'correct'.

—E.T. Jaynes^[1]

Explanation and implications

In case (1) above, the conditional probability that the longitude Φ lies in a set E given that θ = 0 can be written P(Φ ∈ E | θ = 0). Elementary probability theory suggests this can be computed as P(Φ ∈ E and θ=0)/P(θ=0), but that expression is not well-defined since P(θ=0) = 0. Measure theory provides a way to define a conditional probability, using the family of events R_ab = {θ : a < θ < b} which are horizontal rings consisting of all points with latitude between a and b. R_ab can be used to construct a function f_E(θ) = P(Φ ∈ E|θ=θ), which can then be evaluated at f_E(0) to give P(Φ ∈ E|θ=0). See conditional expectation for more information.

The resolution of the paradox is to notice that in case (2), P(θ ∈ F | Φ=0) is defined using the events L_ab = {Φ : a < Φ < b}, which are vertical wedges (more precisely lunes), consisting of all points whose longitude varies between a and b. So although P(Φ|θ=0) and P(θ|Φ=0) each provide a probability distribution on a great circle, one of them is defined using rings, and the other using lunes. Thus it is not surprising after all that P(Φ|θ=0) and P(θ|Φ=0) have different distributions.

The concept of a conditional probability with regard to an isolated hypothesis whose probability equals 0 is inadmissible. For we can obtain a probability distribution for [the latitude] on the meridian circle only if we regard this circle as an element of the decomposition of the entire spherical surface onto meridian circles with the given poles

—Andrey Kolmogorov^[2]

… the term 'great circle' is ambiguous until we specify what limiting operation is to produce it. The intuitive symmetry argument presupposes the equatorial limit; yet one eating slices of an orange might presuppose the other.

—E.T. Jaynes^[1]

Further example

An implication is that conditional density functions are not invariant under coordinate transformation of the conditioning variable.

Consider two continuous random variables (U,V) with joint density p_UV. Now, let W = V / g(U) for some positive-valued, continuous function g. By change of variables, the joint density of (U,W) is:

Note that W = 0 if and only if V = 0, so it would appear that the conditional distribution of U should be the same under each of these events. However:

whereas

which are not equal unless g is constant.

Notes

References and further reading